Core implementation: Difference between revisions
| (29 intermediate revisions by the same user not shown) | |||
| Line 15: | Line 15: | ||
$\label{eq:taylorexp} | $\label{eq:taylorexp} | ||
\begin{array}{lclrrrr} | \begin{array}{lclrrrr} | ||
f(x_{-k}) &=& f(x_0) | |||
&+& (x_{-k}-x_0)\,f'(x_0) &+& \frac{(x_{-k}-x_0)^2}{2!}\,f''(x_0)+\dots | |||
\\ & \vdots & \\ | |||
f(x_k) &=& f(x_0) | |||
&+& (x_k-x_0)\,f'(x_0) &+& \frac{(x_k-x_0)^2}{2!}\,f''(x_0)+\dots | |||
\end{array}$ | \end{array}$ | ||
| Line 25: | Line 25: | ||
$\vec{f}=\mat{A}\,\vec{df}, \quad | $\vec{f}=\mat{A}\,\vec{df}, \quad | ||
\vec{df}=\mat{A}^{-1}\,\vec{f}, \quad | |||
\vec{f}=\left[\begin{array}{c}f(x_{-k})\\ | |||
\vdots\\ f(x_k)\end{array}\right], \quad | |||
\vec{df}=\left[\begin{array}{c} | |||
f(x_0)\\ f'(x_0)\\ f''(x_0)\\ \vdots \end{array}\right]$ | |||
Derivatives are calculated using weights from the appropriate row of $\mat{A}^{-1}$. | Derivatives are calculated using weights from the appropriate row of $\mat{A}^{-1}$. | ||
| Line 38: | Line 38: | ||
$\begin{eqnarray*} | $\begin{eqnarray*} | ||
\int f(x) \, {\mathrm d}x & = & | |||
\begin{array}{c}(x-x_0)\,f(x_0) + \frac{(x-x_0)^2}{2!}\,f'(x_0) + | |||
\frac{(x-x_0)^3}{3!}\,f''(x_0) + \dots \end{array} | |||
\\ | |||
& = & | |||
[\begin{array}{lll}(x-x_0) & \frac{(x-x_0)^2}{2!} & | |||
\dots \end{array}] \,\, \mat{A}^{-1}\vec{f}\end{eqnarray*}$ | |||
The total integral is approximated by | The total integral is approximated by | ||
| Line 59: | Line 59: | ||
$\label{eq:matmod} | $\label{eq:matmod} | ||
\mat{L}\, \vec{p} = \vec{q},$ | |||
where $\vec{p}$ is unknown. If the matrix operators are formed by linear combinations of the weights in [[#Differentiation]], using only $k$ neighbouring points to each side, they are banded. Boundary conditions are formed in the same way and are placed in the end rows. The equation is solved by forward-backward substitution, using the banded LU-factorisation of $\mat{L}$. | where $\vec{p}$ is unknown. If the matrix operators are formed by linear combinations of the weights in [[#Differentiation]], using only $k$ neighbouring points to each side, they are banded. Boundary conditions are formed in the same way and are placed in the end rows. The equation is solved by forward-backward substitution, using the banded LU-factorisation of $\mat{L}$. | ||
| Line 70: | Line 70: | ||
$A(\theta,z) = | $A(\theta,z) = | ||
\sum_{|k|<K}\sum_{|m|<M}\, A_{km} {\mathrm e}^{{\mathrm i} (\alpha kz + m_0 m\theta)}$ | |||
$A$ real implies $A_{km} = A_{-k,-m}^*$ (coefficients are conjugate-symmetric). It is sufficient to keep only $m\ge 0$, and for $m=0$ keep $k\ge 0$. | $A$ real implies $A_{km} = A_{-k,-m}^*$ (coefficients are conjugate-symmetric). It is sufficient to keep only $m\ge 0$, and for $m=0$ keep $k\ge 0$. | ||
| Line 83: | Line 83: | ||
$\int_0^{2\pi} {\mathrm e}^{{\mathrm i}(m+n)} \, {\mathrm d}\theta | $\int_0^{2\pi} {\mathrm e}^{{\mathrm i}(m+n)} \, {\mathrm d}\theta | ||
= 2\pi \, \delta_{m,-n}\, , | |||
\qquad | |||
\int_0^{\frac{2\pi}{\alpha}} {\mathrm e}^{{\mathrm i}\alpha(k+j)} \, {\mathrm d}z | |||
= \frac{2\pi}{\alpha} \, \delta_{k,-j}$ | |||
=== | === Volume integral === | ||
$E \, = \, | $E \, = \, | ||
\int A \, {\mathrm d}V | |||
\, = \, | |||
\frac{4\pi^2}{\alpha} \, \int A_{00} \, r\,{\mathrm d}r$ | |||
=== Energy integral === | |||
$E \, = \, | $E \, = \, | ||
{\textstyle \frac1{2}} \int \vec{A} \cdot \vec{A} \, {\mathrm d}V | |||
\, = \, | |||
\frac{2\pi^2}{\alpha} \, \sum_{km} | |||
\int |\vec{A}_{km}|^2 \, r\,{\mathrm d}r$ | |||
$E = \sum_{m\ge 0} E_m, | |||
\qquad | |||
E_m = | |||
\left\{ | |||
\begin{array}{ll} | |||
\displaystyle | |||
\frac{2\pi^2}{\alpha}\int\vec{A}_{00}^2 \, r \, {\mathrm d}r | |||
+ \frac{4\pi^2}{\alpha} \sum_{k>0} | |||
\int|\vec{A}_{k0}^2| \, r \, {\mathrm d}r, | |||
& m=0, \\[15pt] | |||
\displaystyle | |||
\frac{4\pi^2}{\alpha} \sum_k | |||
\int |\vec{A}_{km}|^2 \, r \, {\mathrm d}r, | |||
& m>0 . | |||
\end{array} | |||
\right.$ | |||
= Temporal discretisation = | = Temporal discretisation = | ||
Temporal discritisation is via a second-order Predictor-Corrector scheme, with Euler predictor for the nonlinear terms and Crank-Nicolson corrector. The linear viscous term is treated implicitly with the Crank-Nicolson term. | |||
== PPE-formulation with correct boundary conditions == | == PPE-formulation with correct boundary conditions == | ||
An influence-matrix technique is used to avoid issues in satisfying the boundary conditions. See [[The_PPE_formulation]]. | |||
== Predictor-corrector == | == Predictor-corrector == | ||
| Line 189: | Line 133: | ||
$\label{eq:harmmod} | $\label{eq:harmmod} | ||
(\partial_{t} - \nabla^2) f = N,$ | |||
where nonlinear terms have been evaluated on each radial point by the transform method, and is solved as in [[#Matrix_representation_of_linear_operators]]. The predictor at time $t_q$, with Euler nonlinear terms and implicitness $c$ | where nonlinear terms have been evaluated on each radial point by the transform method, and is solved as in [[#Matrix_representation_of_linear_operators]]. The predictor at time $t_q$, with Euler nonlinear terms and implicitness $c$ | ||
$\frac{f_1^{q+1}-f^q}{\Delta t} | $\frac{f_1^{q+1}-f^q}{\Delta t} | ||
- \left( c\nabla^2 f_1^{q+1} + (1-c)\nabla^2 f^q \right) | |||
= N^q ,$ | |||
$\left( \frac1{\Delta t} - c\nabla^2 \right) f_1^{q+1} | $\left( \frac1{\Delta t} - c\nabla^2 \right) f_1^{q+1} | ||
= \left( \frac1{\Delta t} + (1-c)\nabla^2 \right) f^q + N^q .$ | |||
Corrector iterations are | Corrector iterations are | ||
$\left( \frac1{\Delta t} - c\nabla^2 \right) f_{j+1}^{q+1} | $\left( \frac1{\Delta t} - c\nabla^2 \right) f_{j+1}^{q+1} | ||
= \left( \frac1{\Delta t} + (1-c)\nabla^2 \right) f^q | |||
+ c\,N_j^{q+1} + (1-c)\, N^q ,$ | |||
or equivalently, for the correction $f_{corr} = f_{j+1}^{q+1} - f_j^{q+1}$ | or equivalently, for the correction $f_{corr} = f_{j+1}^{q+1} - f_j^{q+1}$ | ||
$\left( \frac1{\Delta t} - c\nabla^2 \right) f_{corr} | $\left( \frac1{\Delta t} - c\nabla^2 \right) f_{corr} | ||
= c\,N_j^{q+1} - c\, N_{j-1}^{q+1} ,$ | |||
where $j=1,2,\dots$ and $N_0^{q+1}=N^q$. The size of the correction $\|f_{corr}\|$ must reduce at each iteration. For $c=\frac1{2}$ the scheme is second order such that $\|f_{corr}\| \sim \Delta t^2$. Stability is improved without observable degradation in accuracy using $c=0.501$ . | where $j=1,2,\dots$ and $N_0^{q+1}=N^q$. The size of the correction $\|f_{corr}\|$ must reduce at each iteration. For $c=\frac1{2}$ the scheme is second order such that $\|f_{corr}\| \sim \Delta t^2$. Stability is improved without observable degradation in accuracy using $c=0.501$ . | ||
| Line 216: | Line 160: | ||
$\Delta t = \mathrm{C} \, \min(\Delta \, / \, |\vec{v}| ) , | $\Delta t = \mathrm{C} \, \min(\Delta \, / \, |\vec{v}| ) , | ||
\qquad | |||
0<\mathrm{C}<1,$ | |||
where $\mathrm{C}$ is the Courant number. | where $\mathrm{C}$ is the Courant number. | ||
| Line 224: | Line 168: | ||
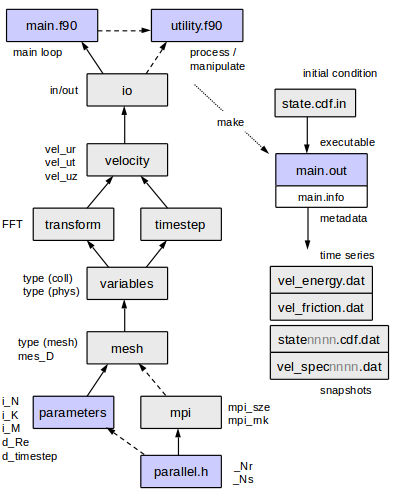
= The code structure = | = The code structure = | ||
[[File:modules4.png]] | |||
== Overview of program files == | == Overview of program files == | ||
* '''<tt>parameters.f90</tt>''' declaration and values of parameters. | * '''<tt>parameters.f90</tt>''' declaration and values of parameters. | ||
* '''<tt>parallel.h</tt>''' | * '''<tt>parallel.h</tt>''' macros for parallelisation; definition of loops for parallel+serial cases <tt>_loop_km_begin</tt> etc. | ||
* '''<tt>mpi.f90</tt>''' mpi initialisation. | * '''<tt>mpi.f90</tt>''' mpi initialisation. | ||
* '''<tt>main.f90</tt>''' core initialisation, main timestepping loop, clean up at end. | * '''<tt>main.f90</tt>''' core initialisation, main timestepping loop, clean up at end. | ||
| Line 237: | Line 183: | ||
* '''<tt>velocity.f90</tt>''' functions related to the velocity field; implementation of the timestepping and influence matrix method. | * '''<tt>velocity.f90</tt>''' functions related to the velocity field; implementation of the timestepping and influence matrix method. | ||
* '''<tt>io.f90</tt>''' Input-Output: loading and saving of data. | * '''<tt>io.f90</tt>''' Input-Output: loading and saving of data. | ||
Each of the files contains a '<tt>module</tt>', declaring variables that may be used in other code via '<tt>use modulename</tt>'. With the exception of the fundamental parameters, the first three letters of the module name are used as a prefix in the name of public variables, to make the location of their declaration clear (see following section). | |||
== Naming conventions == | == Naming conventions == | ||
| Line 287: | Line 235: | ||
== Ordering the Fourier modes == | == Ordering the Fourier modes == | ||
$A = \sum_{ | $A = \sum_{|k|<K}\sum_{|m|<M}\, A_{km} {\mathrm e}^{{\mathrm i}(\alpha kz + m_0 m\theta)},$ | ||
Coefficients are stored | Coefficients $A_{km}$ are stored in an order according to the following loop, where | ||
rather than two indices <tt>k</tt> and <tt>m</tt>, the single index <tt>nh</tt> labels the modes: | rather than two indices <tt>k</tt> and <tt>m</tt>, the single index <tt>nh</tt> labels the modes: | ||
| Line 299: | Line 247: | ||
nh = nh+1 | nh = nh+1 | ||
...</pre> | ...</pre> | ||
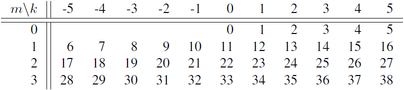
The index nh is as in the following table for the case K=6, M=4: | |||
[[File:Fourier_km.png|404px]] | |||
NOTES: | NOTES: | ||
* Loops for | * <tt>nh = (2*K-1)*m + k</tt>. | ||
* This loop | * Loops for <tt>m<0</tt> are skipped. Values of coefficients for <tt>m<0</tt> are inferred from the conjugate symmetric property, $A_{km}=A_{-k,-m}^*$. Similarly for <tt>k<0</tt> when <tt>m==0</tt>. | ||
* This loop is a predefined macro in <tt>parallel.h</tt>. The macro <tt>_loop_km_begin</tt> replaces the double-loop above (or its equivalent for parallel computation). | |||
== Data types == | == Data types == | ||
The data types below consist of logical data groups to facilitate the passing of data between functions. For clarity, in the following text they are defined as though we were working on a single processor. See [[#Modifications_for_the_parallel_implementation|Parallel]] regarding subtle differences in the definitions due to parallelisation. | The data types below consist of logical data groups to facilitate the passing of data between functions. For clarity, in the following text they are defined as though we were working on a single processor. See [[#Modifications_for_the_parallel_implementation|Parallel]] regarding subtle differences in the definitions due to parallelisation. | ||
The most important data types are <tt>type (coll) </tt> and <tt> type (phys)</tt>. The transform between the two types is achieved with calls to <tt>tra_coll2phys(...)</tt>, <tt>tra_phys2coll(...)</tt>. | |||
=== coll, spec — storage of coefficients === | === coll, spec — storage of coefficients === | ||
| Line 323: | Line 278: | ||
double precision :: Im(0:i_H1, i_N) | double precision :: Im(0:i_H1, i_N) | ||
end type spec</pre> | end type spec</pre> | ||
=== phys — real space data === | === phys — real space data === | ||
| Line 336: | Line 290: | ||
=== rdom — the radial domain === | === rdom — the radial domain === | ||
The <tt>type (rdom)</tt> contains information the radial domain. The public variable <tt>mes_D</tt> is declared in <tt>meshs.f90</tt>. Data includes the number of radial points <tt>mes_D%N</tt>, powers of $r$, $r_n^p$=<tt>mes_D%r(n,p)</tt>, weights for integration | The <tt>type (rdom)</tt> contains information about the radial domain. The public variable <tt>mes_D</tt> is declared in <tt>meshs.f90</tt>. Data includes the number of radial points <tt>mes_D%N</tt>, powers of $r$, $r_n^p$=<tt>mes_D%r(n,p)</tt>, weights for integration | ||
$\int_0^1 f(r)\,r\,{\mathrm d}r$=<tt>dot_product(f(1:i_N),mes_D%intrdr)</tt>, matrices for taking the $p^{\mathrm{th}}$ derivative and more: | $\int_0^1 f(r)\,r\,{\mathrm d}r$=<tt>dot_product(f(1:i_N),mes_D%intrdr)</tt>, matrices for taking the $p^{\mathrm{th}}$ derivative and more: | ||
| Line 363: | Line 317: | ||
== Modifications for the parallel implementation == | == Modifications for the parallel implementation == | ||
=== Practical things to remember === | |||
The code has been parallelised using the Message Passing Interface (MPI) in a way designed to be as unintrusive as possible. Sections of the code with special MPI function calls are separated from the serial sections by preprocessor directives. The number of processors is given by the parameter <tt>_Np=_Nr*_Ns</tt> set in <tt>parallel.h</tt>. The rank of a process is given by <tt>mpi_rnk</tt> declared in <tt>mpi.f90</tt>, and <tt>mpi_sze</tt>$=$<tt>_Np</tt>. | The code has been parallelised using the Message Passing Interface (MPI) in a way designed to be as unintrusive as possible. Sections of the code with special MPI function calls are separated from the serial sections by preprocessor directives. The number of processors is given by the parameter <tt>_Np=_Nr*_Ns</tt> set in <tt>parallel.h</tt>. The rank of a process is given by <tt>mpi_rnk</tt> declared in <tt>mpi.f90</tt>, and <tt>mpi_sze</tt>$=$<tt>_Np</tt>. | ||
For modest parallelisations, it is recommended to vary <tt>_Nr</tt> and to keep <tt>_Ns=1</tt> (radial split only). This ensures a couple of conditions are met that could easily be forgotten when setting up a run | For modest parallelisations, it is recommended to vary <tt>_Nr</tt> and to keep <tt>_Ns=1</tt> (radial split only). This ensures a couple of conditions are met that could easily be forgotten when setting up a run, namely that <tt>_Ns</tt> must divide both <tt>i_Z</tt> and <tt>i_M</tt>. | ||
=== How the data is distributed === | |||
The linear parts of the code (evaluating curls, gradients and matrix inversions for the timestepping) involve operations that do not couple Fourier modes. The <tt>type (coll)</tt> holds all radial points for a subset of Fourier modes - the Fourier modes are distributed over the cores. | |||
Products are evaluated in physical space. Here the data is split over <tt>_Nr</tt> sections in $r$ and over <tt>_Ns</tt> sections in $z$. The <tt>type (phys)</tt> holds all azimuthal points for a | |||
given subsection in $r$ and $z$. The following is an example of rank id numbers (<tt>mpi_rnk</tt>) for the case <tt>_Nr=3</tt>, <tt>_Ns=4</tt> ($r$ downwards, $z$ left to right): | |||
0 3 6 9 | |||
1 4 7 10 | |||
2 5 8 11 | |||
In physical space, | |||
* Two cores have data for the same $z$-section if <tt>rank1/_Nr==rank2/_Nr</tt> (integer arithmetic). | |||
* Two cores have data for the same $r$-section if <tt>modulo(rank1,_Nr)==modulo(rank2,_Nr)</tt>. | |||
=== How the code is adapted === | |||
In the definition of <tt>type (coll)</tt> the parameter <tt>i_H1</tt> is replaced by <tt>i_pH1</tt>. | |||
In the definition of <tt>type (phys)</tt> the parameters <tt>i_N,i_Z</tt> are replaced by <tt>i_pN,i_pZ</tt>. | |||
<tt>i_pH1</tt> is the maximum number of modes on an individual core. The variable <tt>var_H</tt> has elements to determine which harmonics are on which processor. The elements <tt>pH0</tt> and <tt>pH1</tt> are the zeroth index and the number of harmonics for the local process, minus one. The corresponding values for all processors are stored in the arrays <tt>pH0_(rank)</tt> and <tt>pH1_(rank)</tt>. For a variable of <tt>type (coll)</tt>, valid values for the harmonic index in <tt>Re(n,nh)</tt> are <tt>nh=0..pH1</tt> but refer to the indices <tt>nh=pH0..pH0+pH1</tt> of the serial case, see [[#Ordering_the_Fourier_modes]]. | |||
In physical space <tt>i_pN</tt> is the maximum number of radial points for each process. The location of the radial subdomain on the local processor is given by additional elements of the variable <tt>mes_D</tt>. The elements <tt>pNi</tt> and <tt>pN</tt> are the location of the first (inner) radial point and the number of points. The values for all processors are stored in the arrays <tt>pNi_(rank)</tt> and <tt>pN_(rank)</tt>. For a variable of <tt>type (spec)</tt>, valid values for the radial index in <tt>Re(nh,n)</tt> are <tt>n</tt>=<tt>1..pN</tt> which refer to the indices of $r_n$, where $n$=<tt>pNi..pNi+pN-1</tt>. | |||
Also in physical space <tt>i_pZ</tt> is exactly the number axial points held by the core. Logically, the local index <tt>k</tt> in <tt>[0,i_pZ-1]</tt>corresponds to index <tt>(mpi_rnk/_Ns)*i_pZ + k</tt> (integer arithmetic) in <tt>[0,i_Z-1]</tt>. | |||
The bulk of communication occurs during the data transposes in the functions <tt>var_coll2spec()</tt> and <tt>var_spec2coll()</tt>. For <tt>_Np=_Nr | The bulk of communication occurs during the data transposes in the functions <tt>var_coll2spec()</tt> and <tt>var_spec2coll()</tt>. For the case <tt>_Np=_Nr, _Ns=1</tt> the data is transferred in <tt>_Np-1</tt> steps. At each step each processor sends and receives a block of data, the source and destination are selected systematically as set in the following loop: | ||
<pre> do step = 1, mpi_sze-1 | <pre> do step = 1, mpi_sze-1 | ||
| Line 379: | Line 356: | ||
...</pre> | ...</pre> | ||
=== How the parallelisation works === | |||
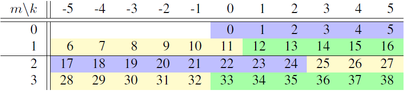
In the Fourier space, all radial points for a particular Fourier mode are located on the same processor, separate modes may be located on separate processes. For the case <tt>K=6, M=4, _Ns=2, _Nr=3,</tt> the modes are split over <tt>_Np=6</tt> cores (<tt>mpi_rnk=0..5</tt>) indicated by the coloured sections in the following table: | |||
[[File:Fourier_km_par.png|404px]] | |||
Here for <tt>_Ns=2</tt> the m are split 0,1 and 2,3, then each section is split into <tt>_Nr=3</tt> sections indicated by the colours. | |||
For <tt>_Ns=2</tt>, two sets each of three cores may be denoted | |||
$\{c_0,c_1,c_2\}$ and $\{c_3,c_4,c_5\}$. | |||
Prior to an FFT, the core $c_0$ gathers all Fourier coefficients from within the first set for a given | |||
subset of radial points -- doing this for each core constitutes a transpose with in the set. | |||
Having gathered these coefficients, sufficient data is present to perform the axial FFTs | |||
(summing over the k for a given m). | |||
Now three sets of cores may be identified, arranged to have data for common | |||
radial points in each set, $\{c_0,c_3\}$, $\{c_1,c_4\}$, $\{c_2,c_5\}$. | |||
Within each set m is distributed, with | |||
m=0,1 is on one core m=2,3 on the other. Gathering the m for a | |||
given subsection of axial points, constitutes a second transpose within each of these | |||
sets. Finally the azimuthal FFTs may be performed (sum over m). | |||
The resulting data is split by both radial and axial position, whilst data for all azimuthal points are present on a given core. | |||
In the double parallelisation two transposes are required, and the total data sent is | |||
doubled. The number of messages required is | |||
<tt>(_Ns-1)+(_Nr-1)</tt> where <tt>_Np=_Nr*_Ns</tt>. | |||
Note that for a given <tt>_Np</tt>, there are significantly fewer messages for <tt>_Nr,_Ns</tt> approximately equal, versus <tt>_Nr=_Np</tt>, <tt>_Ns=1</tt>. | |||
This can substantially reduce time lost in latency, the time setting up communications. | |||
There are fewer large messages rather many small ones. | |||
Revision as of 15:45, 24 July 2020
$ \renewcommand{\vec}[1]{ {\bf #1} } \newcommand{\bnabla}{ \vec{\nabla} } \newcommand{\Rey}{Re} \def\vechat#1{ \hat{ \vec{#1} } } \def\mat#1{#1} $
Spatial representation
Finite difference stencil — $r$
A function $p(r)$ is represented by the values $p_n=p(r_n)$, where $p(r)$ is evaluated on the $N$ radial points $r_n$; $n=1..N$. There is no point on the axis $r=0$ to avoid singularities in $1/r$ terms. The points are located at the roots of a Tchebyshev polynomial, such that they are clustered near the wall, and slightly so near the axis to compensate for loss of order in the calculation of derivatives. (They are calculated using banded matrices, implying use of fewer points at the axis and boundary).
Differentiation
Taylor expansions about central point $x_0$, $k$ neighbouring points each side
$\label{eq:taylorexp} \begin{array}{lclrrrr} f(x_{-k}) &=& f(x_0) &+& (x_{-k}-x_0)\,f'(x_0) &+& \frac{(x_{-k}-x_0)^2}{2!}\,f(x_0)+\dots \\ & \vdots & \\ f(x_k) &=& f(x_0) &+& (x_k-x_0)\,f'(x_0) &+& \frac{(x_k-x_0)^2}{2!}\,f(x_0)+\dots \end{array}$
The expansions \ref{eq:taylorexp} can be written
$\vec{f}=\mat{A}\,\vec{df}, \quad \vec{df}=\mat{A}^{-1}\,\vec{f}, \quad \vec{f}=\left[\begin{array}{c}f(x_{-k})\\ \vdots\\ f(x_k)\end{array}\right], \quad \vec{df}=\left[\begin{array}{c} f(x_0)\\ f'(x_0)\\ f(x_0)\\ \vdots \end{array}\right]$
Derivatives are calculated using weights from the appropriate row of $\mat{A}^{-1}$.
Integration
Integrating \ref{eq:taylorexp} the indefinite integral may be approximated about $x_0$
$\begin{eqnarray*} \int f(x) \, {\mathrm d}x & = & \begin{array}{c}(x-x_0)\,f(x_0) + \frac{(x-x_0)^2}{2!}\,f'(x_0) + \frac{(x-x_0)^3}{3!}\,f(x_0) + \dots \end{array} \\ & = & [\begin{array}{lll}(x-x_0) & \frac{(x-x_0)^2}{2!} & \dots \end{array}] \,\, \mat{A}^{-1}\vec{f}\end{eqnarray*}$
The total integral is approximated by
$ \frac1{2} \sum_n \int_{x_{n-1}}^{x_{n+1}} f(x) \, {\mathrm d}x$
Matrix representation of linear operators
Linear equations can be written in the matrix form
$\mat{L} \,\vec{p} = \mat{M}\, \vec{q} + \vec{s}.$
$\mat{L}$ and $\mat{M}$ are $N\times N$ matrices representing linear operators. If $\vec{q}$ and $\vec{s}$ are known then the right-hand side is simple to evaluate. Consider the equation
$\label{eq:matmod} \mat{L}\, \vec{p} = \vec{q},$
where $\vec{p}$ is unknown. If the matrix operators are formed by linear combinations of the weights in #Differentiation, using only $k$ neighbouring points to each side, they are banded. Boundary conditions are formed in the same way and are placed in the end rows. The equation is solved by forward-backward substitution, using the banded LU-factorisation of $\mat{L}$.
figure=LU.eps, scale=0.65
Fourier representaion — $\theta$, $z$
Expansion of variables
$A(\theta,z) = \sum_{|k|<K}\sum_{|m|<M}\, A_{km} {\mathrm e}^{{\mathrm i} (\alpha kz + m_0 m\theta)}$
$A$ real implies $A_{km} = A_{-k,-m}^*$ (coefficients are conjugate-symmetric). It is sufficient to keep only $m\ge 0$, and for $m=0$ keep $k\ge 0$.
Implied conditions on the axis
The geometry enforces conditions on each variable at the axis when expanded over Fourier modes in $\theta$. For scalars and the $z$-component of a vector $A_z$, each mode is even in $r$ if $m$ is even, and is odd if $m$ is odd. Each mode for $A_r$ and $A_\theta$ is even in $r$ if $m$ is odd, and is odd if $m$ is even. This implies that either the function or its derivative is zero on the axis.
Orthogonality
Exponentials
$\int_0^{2\pi} {\mathrm e}^{{\mathrm i}(m+n)} \, {\mathrm d}\theta = 2\pi \, \delta_{m,-n}\, , \qquad \int_0^{\frac{2\pi}{\alpha}} {\mathrm e}^{{\mathrm i}\alpha(k+j)} \, {\mathrm d}z = \frac{2\pi}{\alpha} \, \delta_{k,-j}$
Volume integral
$E \, = \, \int A \, {\mathrm d}V \, = \, \frac{4\pi^2}{\alpha} \, \int A_{00} \, r\,{\mathrm d}r$
Energy integral
$E \, = \, {\textstyle \frac1{2}} \int \vec{A} \cdot \vec{A} \, {\mathrm d}V \, = \, \frac{2\pi^2}{\alpha} \, \sum_{km} \int |\vec{A}_{km}|^2 \, r\,{\mathrm d}r$
$E = \sum_{m\ge 0} E_m, \qquad E_m = \left\{ \begin{array}{ll} \displaystyle \frac{2\pi^2}{\alpha}\int\vec{A}_{00}^2 \, r \, {\mathrm d}r + \frac{4\pi^2}{\alpha} \sum_{k>0} \int|\vec{A}_{k0}^2| \, r \, {\mathrm d}r, & m=0, \\[15pt] \displaystyle \frac{4\pi^2}{\alpha} \sum_k \int |\vec{A}_{km}|^2 \, r \, {\mathrm d}r, & m>0 . \end{array} \right.$
Temporal discretisation
Temporal discritisation is via a second-order Predictor-Corrector scheme, with Euler predictor for the nonlinear terms and Crank-Nicolson corrector. The linear viscous term is treated implicitly with the Crank-Nicolson term.
PPE-formulation with correct boundary conditions
An influence-matrix technique is used to avoid issues in satisfying the boundary conditions. See The_PPE_formulation.
Predictor-corrector
The model equation for each Fourier mode is
$\label{eq:harmmod} (\partial_{t} - \nabla^2) f = N,$
where nonlinear terms have been evaluated on each radial point by the transform method, and is solved as in #Matrix_representation_of_linear_operators. The predictor at time $t_q$, with Euler nonlinear terms and implicitness $c$
$\frac{f_1^{q+1}-f^q}{\Delta t} - \left( c\nabla^2 f_1^{q+1} + (1-c)\nabla^2 f^q \right) = N^q ,$
$\left( \frac1{\Delta t} - c\nabla^2 \right) f_1^{q+1} = \left( \frac1{\Delta t} + (1-c)\nabla^2 \right) f^q + N^q .$
Corrector iterations are
$\left( \frac1{\Delta t} - c\nabla^2 \right) f_{j+1}^{q+1} = \left( \frac1{\Delta t} + (1-c)\nabla^2 \right) f^q + c\,N_j^{q+1} + (1-c)\, N^q ,$
or equivalently, for the correction $f_{corr} = f_{j+1}^{q+1} - f_j^{q+1}$
$\left( \frac1{\Delta t} - c\nabla^2 \right) f_{corr} = c\,N_j^{q+1} - c\, N_{j-1}^{q+1} ,$
where $j=1,2,\dots$ and $N_0^{q+1}=N^q$. The size of the correction $\|f_{corr}\|$ must reduce at each iteration. For $c=\frac1{2}$ the scheme is second order such that $\|f_{corr}\| \sim \Delta t^2$. Stability is improved without observable degradation in accuracy using $c=0.501$ .
Timestep control
$\Delta t = \mathrm{C} \, \min(\Delta \, / \, |\vec{v}| ) , \qquad 0<\mathrm{C}<1,$
where $\mathrm{C}$ is the Courant number.
The timestep should also be small enough such that the corrector norm $\|f_{corr}\|$ is satisfactorily small. This may be important for integrating initial transients, but ought not to be the limiting factor in general.
The code structure
Overview of program files
- parameters.f90 declaration and values of parameters.
- parallel.h macros for parallelisation; definition of loops for parallel+serial cases _loop_km_begin etc.
- mpi.f90 mpi initialisation.
- main.f90 core initialisation, main timestepping loop, clean up at end.
- meshs.f90 definition of radial discretisation.
- variables.f90 definition of derived types for spectral- and physical-space data.
- transform.fftw3.f90 transform from collocated spectral space to physical space. Uses fftw3 library.
- timestep.f90 subroutines to set up time stepping matrices.
- velocity.f90 functions related to the velocity field; implementation of the timestepping and influence matrix method.
- io.f90 Input-Output: loading and saving of data.
Each of the files contains a 'module', declaring variables that may be used in other code via 'use modulename'. With the exception of the fundamental parameters, the first three letters of the module name are used as a prefix in the name of public variables, to make the location of their declaration clear (see following section).
Naming conventions
Parameters
Parameters defined within parameters.f90 are given a prefix indicating the data type. For example:
| $N$ | i_N | integer |
| $\Delta t$ | d_timestep | double |
| fixed flux? | b_fixed_flux | boolean |
Note that the naming convention frees the variable name for dummy variables, e.g.:
integer :: n
do n = 1, i_N
...
Public variables
By default variables declared within a module are accessible to any other module or subroutine that uses the module. To ensure that it is clear where a public variable is declared, variables are given a prefix. Examples:
| $\Delta t$ | tim_dt | timestep.f90 |
| $u_r$ | vel_r | velocity.f90 |
Ordering the Fourier modes
$A = \sum_{|k|<K}\sum_{|m|<M}\, A_{km} {\mathrm e}^{{\mathrm i}(\alpha kz + m_0 m\theta)},$
Coefficients $A_{km}$ are stored in an order according to the following loop, where rather than two indices k and m, the single index nh labels the modes:
nh = -1
do m = 0, M-1
m_ = m*Mp
do k = -(K-1), (K-1)
if(m==0 .and. k<0) cycle
nh = nh+1
...
The index nh is as in the following table for the case K=6, M=4:
NOTES:
- nh = (2*K-1)*m + k.
- Loops for m<0 are skipped. Values of coefficients for m<0 are inferred from the conjugate symmetric property, $A_{km}=A_{-k,-m}^*$. Similarly for k<0 when m==0.
- This loop is a predefined macro in parallel.h. The macro _loop_km_begin replaces the double-loop above (or its equivalent for parallel computation).
Data types
The data types below consist of logical data groups to facilitate the passing of data between functions. For clarity, in the following text they are defined as though we were working on a single processor. See Parallel regarding subtle differences in the definitions due to parallelisation.
The most important data types are type (coll) and type (phys). The transform between the two types is achieved with calls to tra_coll2phys(...), tra_phys2coll(...).
coll, spec — storage of coefficients
The collocated data type (coll) is the principle type used for mode-independent operations.
type coll
double precision :: Re(i_N, 0:i_H1)
double precision :: Im(i_N, 0:i_H1)
end type coll
The value Re(n,nh) is the real part of the coefficient for the nh$^{\mathrm{th}}$ harmonic at $r_n$.
The spectral type (spec) is a data type for operations independent at each radial point. It is rarely used other than as a transitory data format between the coll and phys types.
type spec
double precision :: Re(0:i_H1, i_N)
double precision :: Im(0:i_H1, i_N)
end type spec
phys — real space data
The type (phys) is used for data in real space.
type phys
double precision :: Re(0:i_Z-1, 0:i_Th-1, i_N)
end type phys
The element Re(k,m,n) refers to the value at $z_k$, $\theta_m$ and $r_n$.
rdom — the radial domain
The type (rdom) contains information about the radial domain. The public variable mes_D is declared in meshs.f90. Data includes the number of radial points mes_D%N, powers of $r$, $r_n^p$=mes_D%r(n,p), weights for integration $\int_0^1 f(r)\,r\,{\mathrm d}r$=dot_product(f(1:i_N),mes_D%intrdr), matrices for taking the $p^{\mathrm{th}}$ derivative and more:
type rdom
integer :: N
double precision :: r(i_N,i_rpowmin:i_rpowmax)
double precision :: intrdr(i_N)
type (mesh) :: dr(i_KL)
...
end type rdom
mesh, lumesh — storage of banded matrices
The finite-difference stencil has finite width (Finite_Differences) and so matrix operations involve matrices that are banded. The type (mesh), defined in meshs.f90, is used for matrices on the radial mesh involving $kl$ points to either side of each node.
type mesh
double precision :: M(2*i_KL+1, i_N)
end type mesh
For a matrix A, the element M(KL+1+n-j, j) = A(n,j). See the man page for the lapack routine dgbtrf. The LU-factorisation of a banded matrix is also banded:
type lumesh
integer :: ipiv(i_N)
double precision :: M(3*i_KL+1, i_N)
end type lumesh
The element M(2*KL+1+n-j, j) = A(n,j). Pivoting information is stored along with the matrix.
Modifications for the parallel implementation
Practical things to remember
The code has been parallelised using the Message Passing Interface (MPI) in a way designed to be as unintrusive as possible. Sections of the code with special MPI function calls are separated from the serial sections by preprocessor directives. The number of processors is given by the parameter _Np=_Nr*_Ns set in parallel.h. The rank of a process is given by mpi_rnk declared in mpi.f90, and mpi_sze$=$_Np.
For modest parallelisations, it is recommended to vary _Nr and to keep _Ns=1 (radial split only). This ensures a couple of conditions are met that could easily be forgotten when setting up a run, namely that _Ns must divide both i_Z and i_M.
How the data is distributed
The linear parts of the code (evaluating curls, gradients and matrix inversions for the timestepping) involve operations that do not couple Fourier modes. The type (coll) holds all radial points for a subset of Fourier modes - the Fourier modes are distributed over the cores.
Products are evaluated in physical space. Here the data is split over _Nr sections in $r$ and over _Ns sections in $z$. The type (phys) holds all azimuthal points for a given subsection in $r$ and $z$. The following is an example of rank id numbers (mpi_rnk) for the case _Nr=3, _Ns=4 ($r$ downwards, $z$ left to right):
0 3 6 9 1 4 7 10 2 5 8 11
In physical space,
- Two cores have data for the same $z$-section if rank1/_Nr==rank2/_Nr (integer arithmetic).
- Two cores have data for the same $r$-section if modulo(rank1,_Nr)==modulo(rank2,_Nr).
How the code is adapted
In the definition of type (coll) the parameter i_H1 is replaced by i_pH1.
In the definition of type (phys) the parameters i_N,i_Z are replaced by i_pN,i_pZ.
i_pH1 is the maximum number of modes on an individual core. The variable var_H has elements to determine which harmonics are on which processor. The elements pH0 and pH1 are the zeroth index and the number of harmonics for the local process, minus one. The corresponding values for all processors are stored in the arrays pH0_(rank) and pH1_(rank). For a variable of type (coll), valid values for the harmonic index in Re(n,nh) are nh=0..pH1 but refer to the indices nh=pH0..pH0+pH1 of the serial case, see #Ordering_the_Fourier_modes.
In physical space i_pN is the maximum number of radial points for each process. The location of the radial subdomain on the local processor is given by additional elements of the variable mes_D. The elements pNi and pN are the location of the first (inner) radial point and the number of points. The values for all processors are stored in the arrays pNi_(rank) and pN_(rank). For a variable of type (spec), valid values for the radial index in Re(nh,n) are n=1..pN which refer to the indices of $r_n$, where $n$=pNi..pNi+pN-1.
Also in physical space i_pZ is exactly the number axial points held by the core. Logically, the local index k in [0,i_pZ-1]corresponds to index (mpi_rnk/_Ns)*i_pZ + k (integer arithmetic) in [0,i_Z-1].
The bulk of communication occurs during the data transposes in the functions var_coll2spec() and var_spec2coll(). For the case _Np=_Nr, _Ns=1 the data is transferred in _Np-1 steps. At each step each processor sends and receives a block of data, the source and destination are selected systematically as set in the following loop:
do step = 1, mpi_sze-1
dest = modulo(mpi_rnk+step, mpi_sze)
src = modulo(mpi_rnk-step+mpi_sze, mpi_sze)
...
How the parallelisation works
In the Fourier space, all radial points for a particular Fourier mode are located on the same processor, separate modes may be located on separate processes. For the case K=6, M=4, _Ns=2, _Nr=3, the modes are split over _Np=6 cores (mpi_rnk=0..5) indicated by the coloured sections in the following table:
Here for _Ns=2 the m are split 0,1 and 2,3, then each section is split into _Nr=3 sections indicated by the colours.
For _Ns=2, two sets each of three cores may be denoted $\{c_0,c_1,c_2\}$ and $\{c_3,c_4,c_5\}$. Prior to an FFT, the core $c_0$ gathers all Fourier coefficients from within the first set for a given subset of radial points -- doing this for each core constitutes a transpose with in the set. Having gathered these coefficients, sufficient data is present to perform the axial FFTs (summing over the k for a given m). Now three sets of cores may be identified, arranged to have data for common radial points in each set, $\{c_0,c_3\}$, $\{c_1,c_4\}$, $\{c_2,c_5\}$. Within each set m is distributed, with m=0,1 is on one core m=2,3 on the other. Gathering the m for a given subsection of axial points, constitutes a second transpose within each of these sets. Finally the azimuthal FFTs may be performed (sum over m). The resulting data is split by both radial and axial position, whilst data for all azimuthal points are present on a given core.
In the double parallelisation two transposes are required, and the total data sent is doubled. The number of messages required is (_Ns-1)+(_Nr-1) where _Np=_Nr*_Ns. Note that for a given _Np, there are significantly fewer messages for _Nr,_Ns approximately equal, versus _Nr=_Np, _Ns=1. This can substantially reduce time lost in latency, the time setting up communications. There are fewer large messages rather many small ones.